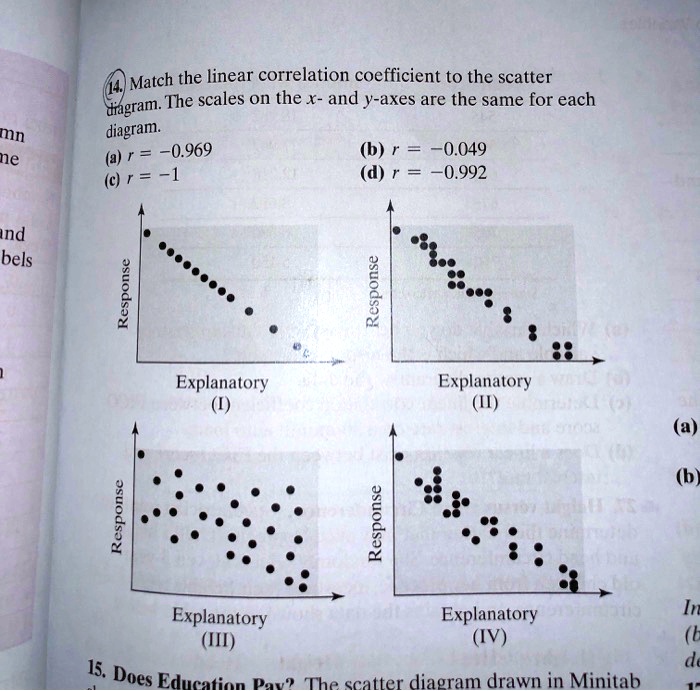
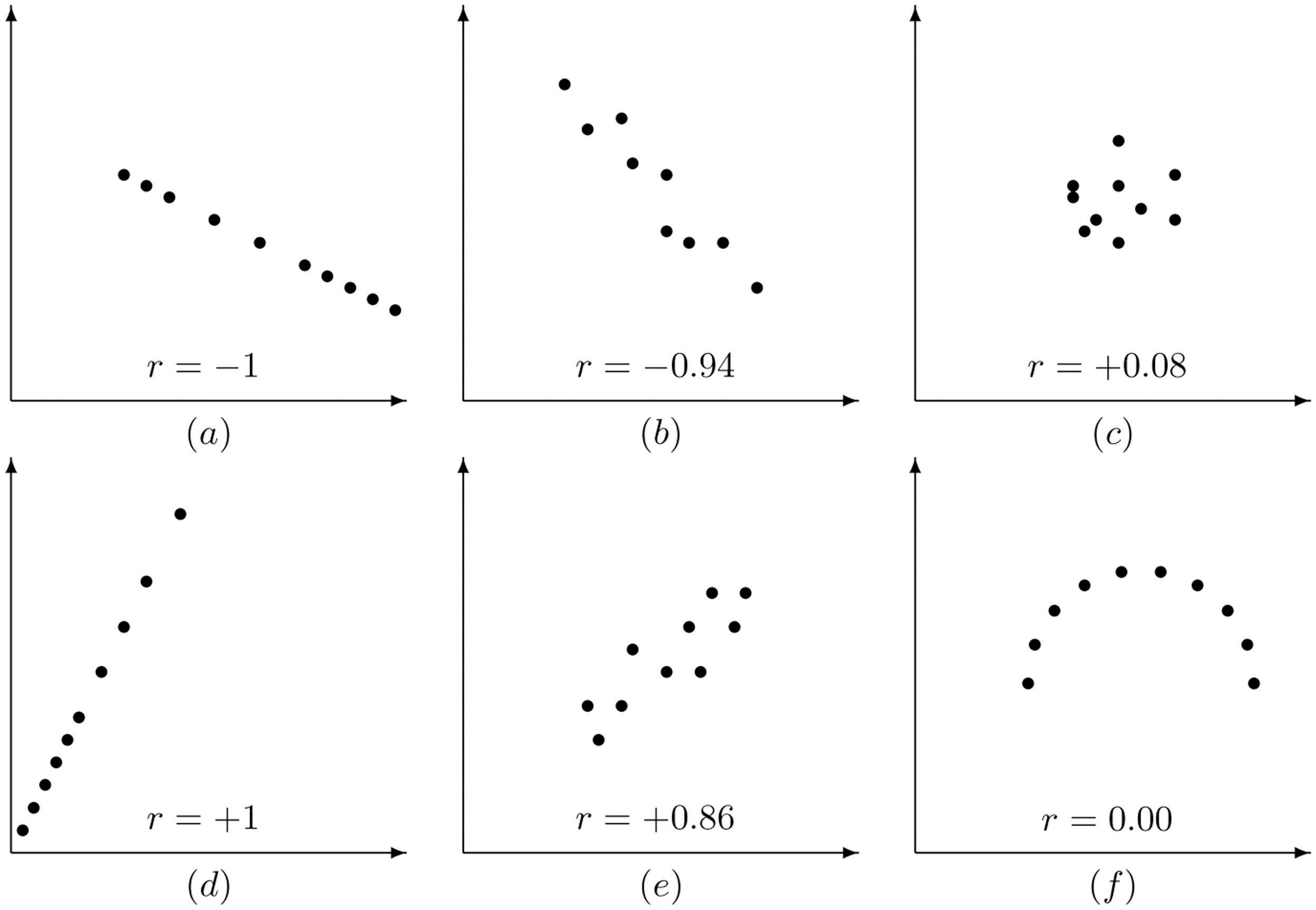
36 match the linear correlation coefficient to the scatter diagram.
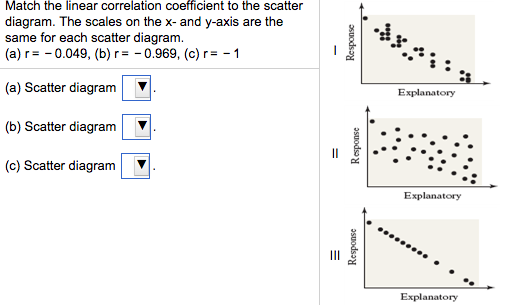
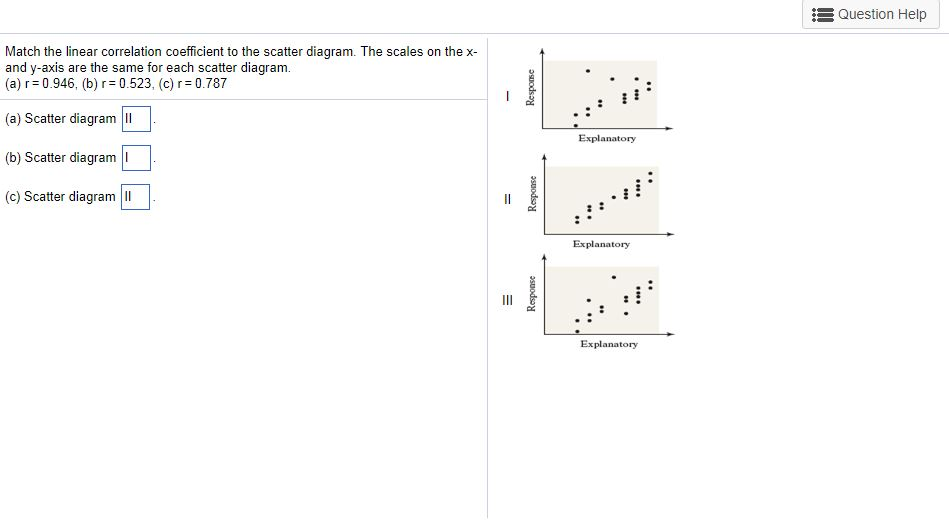
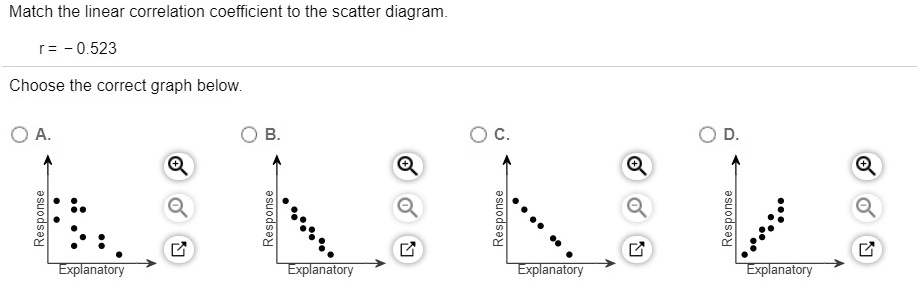
27 Jun 2014 — Match the linear correlation coefficient to the scatter diagram. The scales on the x- and y- axes are the same for each diagram.1 answer · Top answer: Well, without seeing the diagrams: (A) r = -.969 --> points will be tightly scattered about a line with slope -1 (B) r = -.049 --> points will almost ...
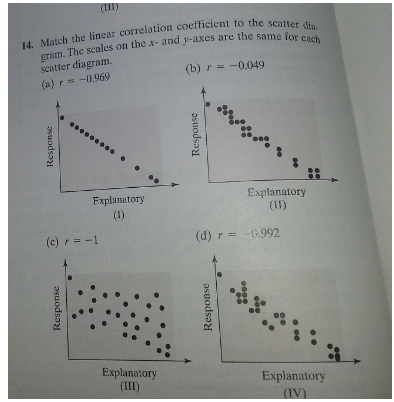
Match the linear correlation coefficient to the scatter diagram. The scales on the x- and y-axis are the same for each scatter diagram (a)r= - 1.1 answer · Top answer: Using the given scatter diagram, a) Scatter diagram I That is r-0.969 Explanatory aoday b) Scatter diagram III That is r=-1 Esplansory c) Scatter diagram ...
Pearson correlation coefficient is the most and widely used.which measures the strength of the linear relationship between normally distributed variables. When the variables are not normally ...
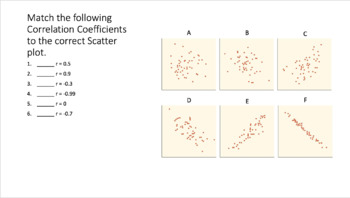
Match the linear correlation coefficient to the scatter diagram.
What symbol is used for the Pearson correlation coefficient, which shows the strength of the relation between two variables? r. Which of these statements correctly describes the values that can be assumed by the correlation coefficient, r? It can be any number from -1 to +1, inclusive. The formula for the correlation coefficient is n sx Y-Y. n = number of paired observations sx = …
a measure of the strength of the linear relationship between two variables If there is absolutely no relationship between the two sets of variables, Pearson's r is zero. A correlation coefficient r close to 0 (say, .08) shows that the linear relationship is quite weak.-1 <= r <= 1
30/10/2014 · This is further confirmed by looking at the scatter diagram in Figure 1, which shows that the quadratic trend line is a better bit for the data than the linear trend line. (To display the quadratic trend line select Layout > Analysis|Trendline and then More Trendline Options… On the display box which appears choose Polynomial trendline of Order 2.) Figure 2 also shows that …
Match the linear correlation coefficient to the scatter diagram..
Look at a scatter plot and estimate a correlation coefficient value and interpret as a strong positive, strong negative, etc... Rating: 5 · 2 reviews
10/02/2021 · Match each graph with its correlation coefficient. Explain your reasoning. Answer: Question 27. ANALYZING RELATIONSHIPS The table shows the grade point averages y of several students and the numbers x of hours they spend watching television each week. a. Use a graphing calculator to find an equation of the line of best fit. Identify and ...
4 answersworking with linear correlation coefficients and scatter diagrams, we may want to try to identify what the strength and direction of relationship is just ...
15/02/2021 · USING TOOLS In Exercises 19–24, use the linear regression feature on a graphing calculator to find an equation of the line of best fit for the data. Find and interpret the correlation coefficient. Question 19. Answer: Question 20. Answer: Question 21. Answer: Question 22. Answer: Question 23. Answer: Question 24. Answer: Question 25.
The linear correlation coefficient has the following properties, illustrated in Figure 10.4 "Linear Correlation Coefficient ": . The value of r lies between −1 and 1, inclusive.; The sign of r indicates the direction of the linear relationship between x and y: . If r < 0 then y tends to decrease as x is increased.; If r > 0 then y tends to increase as x is increased.
Learn with an example. question. Match each correlation coefficient to the appropriate scatter plot. The line in each scatter plot is the least squares ...
10/02/2021 · (b) Identify and interpret the correlation coefficient. (c) Interpret the slope and y-intercept of the line of best fit. Answer: b. Correlation coefficient is -0.9636. So, the relation is a strong negative correlation. c. Slope is -9.58788, y-intercept is 844.54545. Explanation: a. Using the linear regression feature the equation y = -9.8x ...
Transcribed image text: Match the linear correlation coefficient to the scatter diagram. The scales on the x- and y-axes are the same for each gram.
These videos cover the Pearson Coefficient of Linear Correlation, or r-value, which basically tells you if your scatter plot (or plots) of data pairs lies along a line or not. Also covered are hypothesis testing of linear correlation, and calculating r on your calculator.
The scatter diagram for this data is as follows. We have also included the linear trend line that seems to best match the data. We will study this further in Linear Regression. Figure 2 – Scatter diagram for Example 1. Next, we calculate the correlation coefficient of the sample using the CORREL function: r = CORREL(R1, R2) = -.713


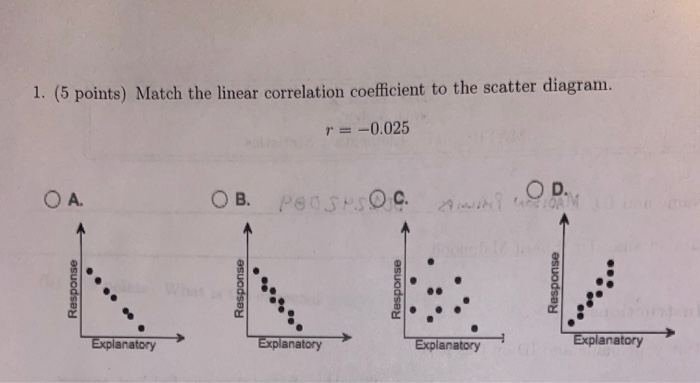

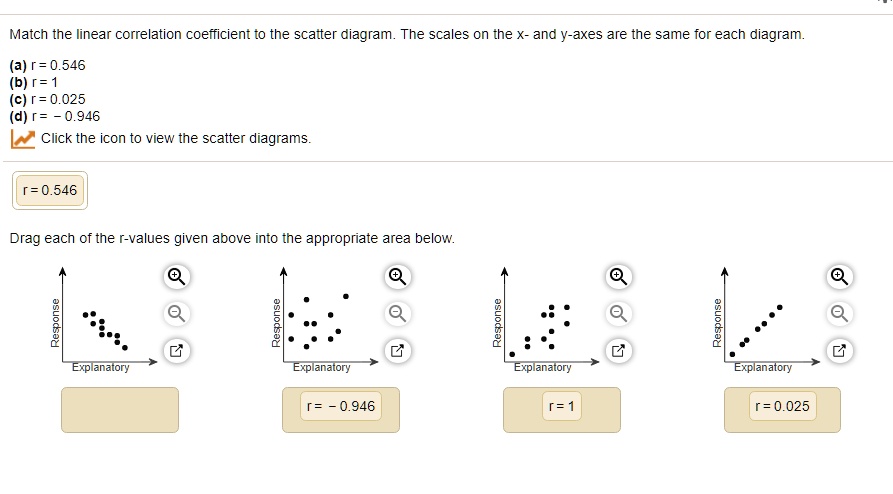

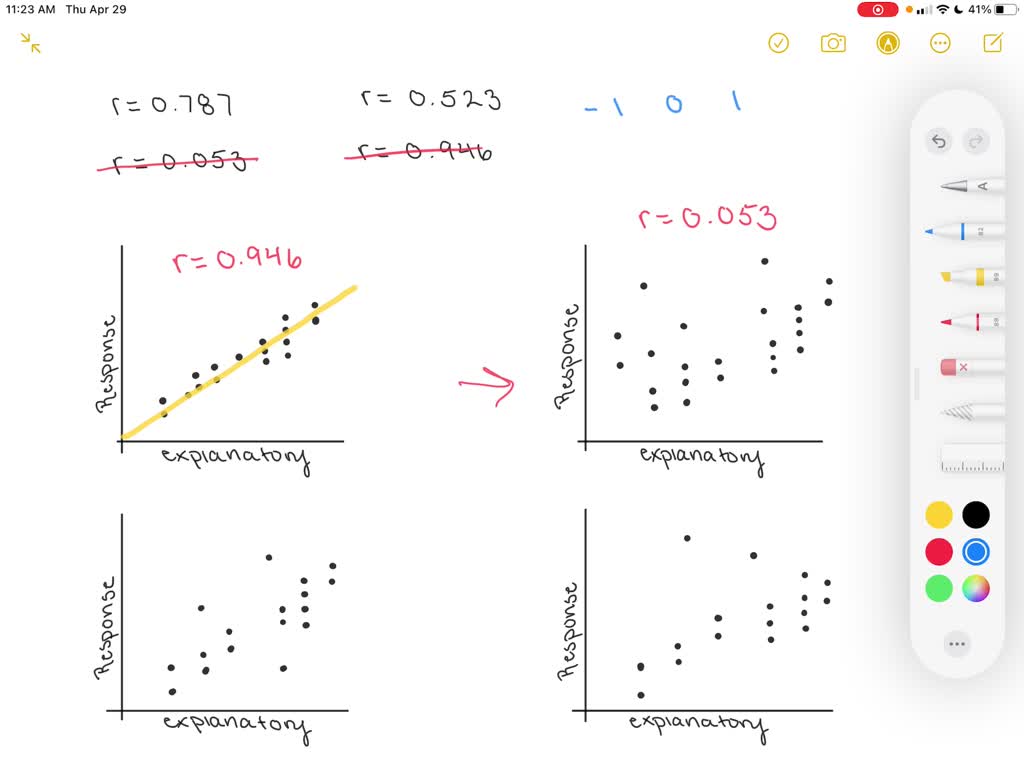
![Solved] Match the coefï¬cient of determination to the scatter ...](https://s3.amazonaws.com/si.question.images/image/images7/445-M-S-D-A(1102).png)
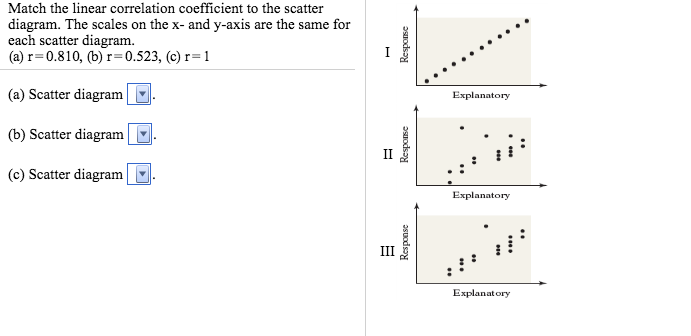
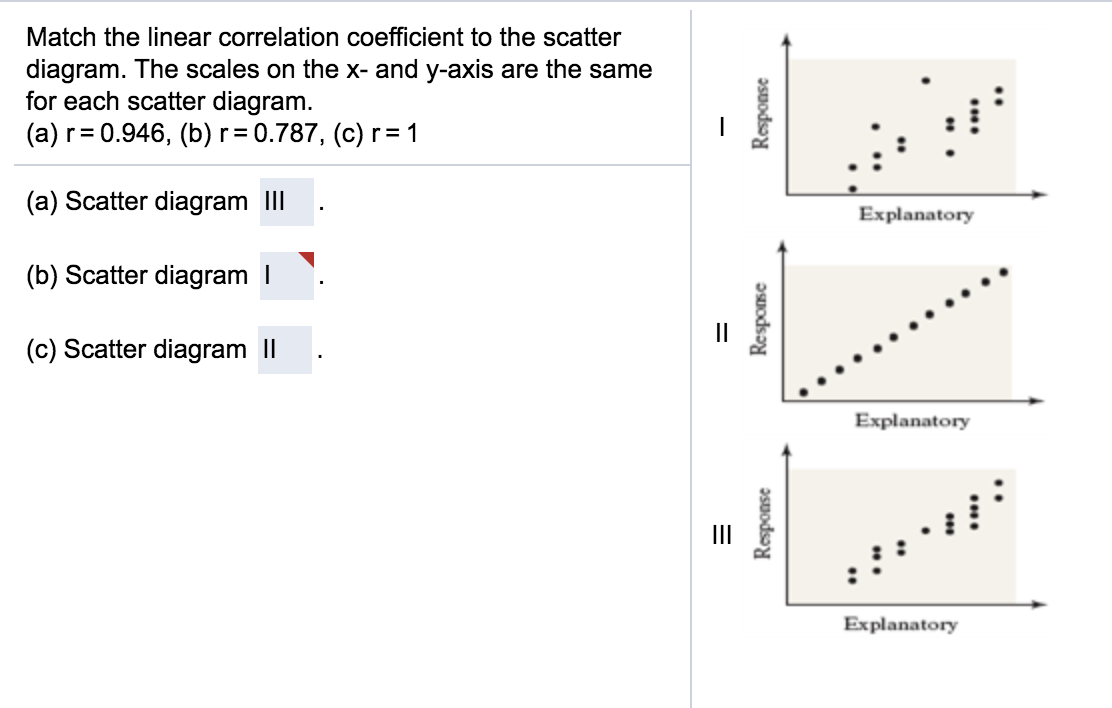
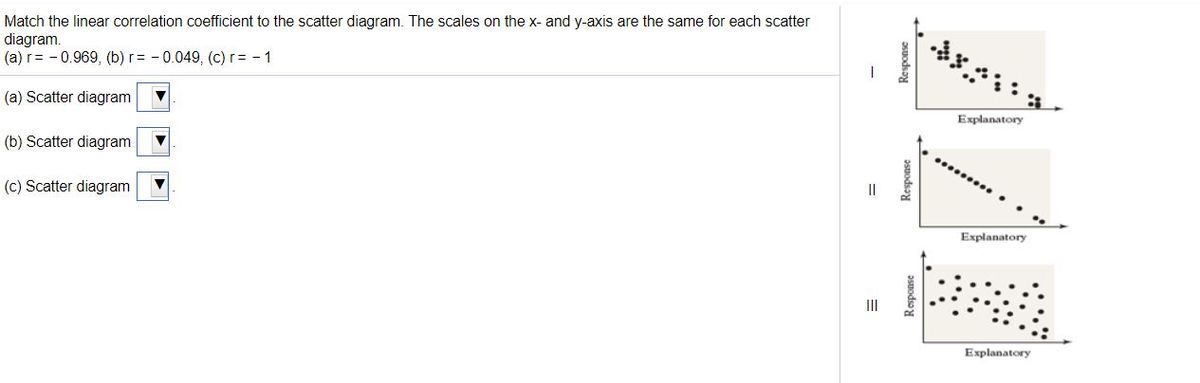
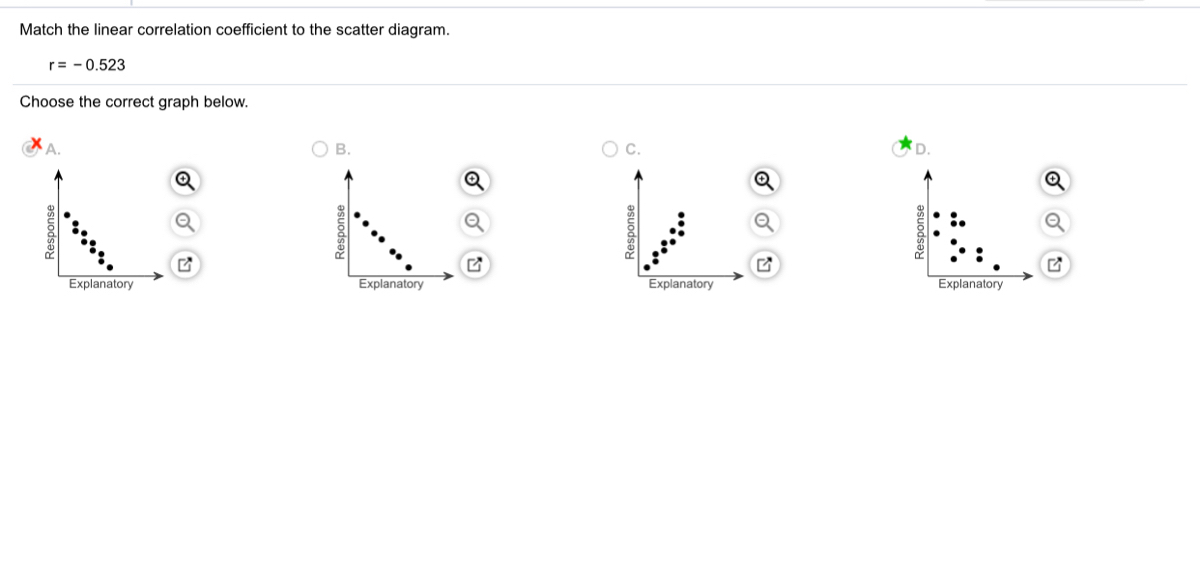
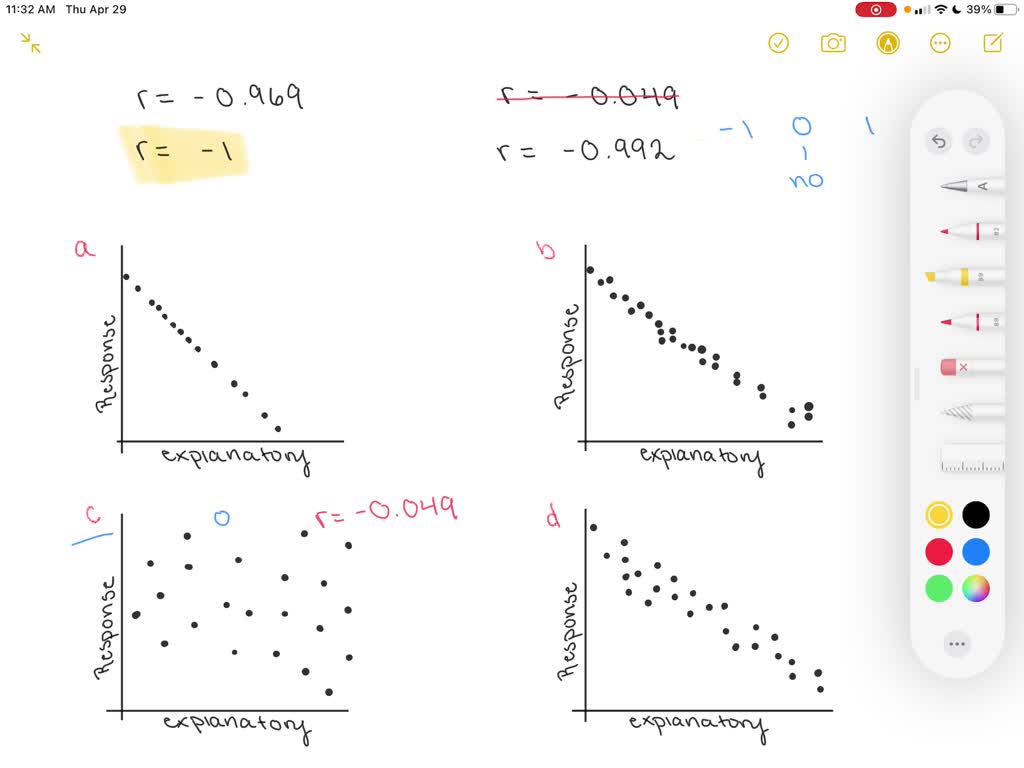
![Solved] Match the linear correlation coefï¬cient to the scatter ...](https://s3.amazonaws.com/si.question.images/image/images7/445-M-S-D-A(1043).png)
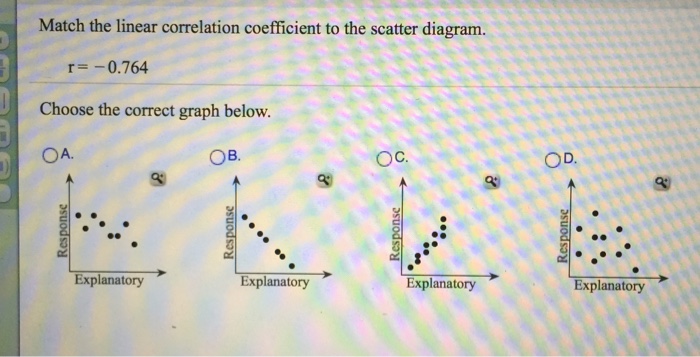

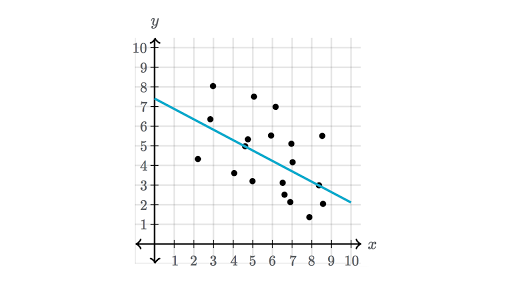
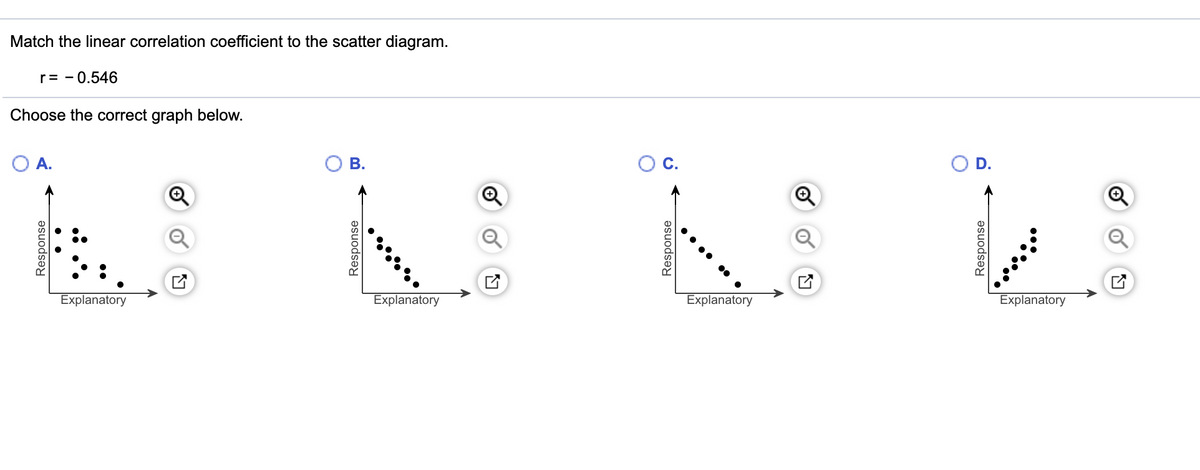
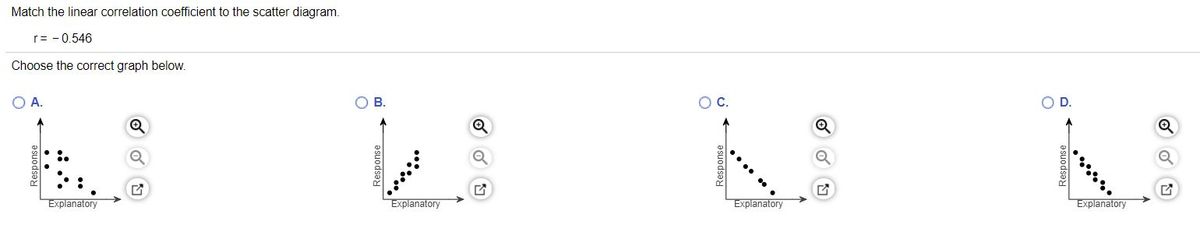
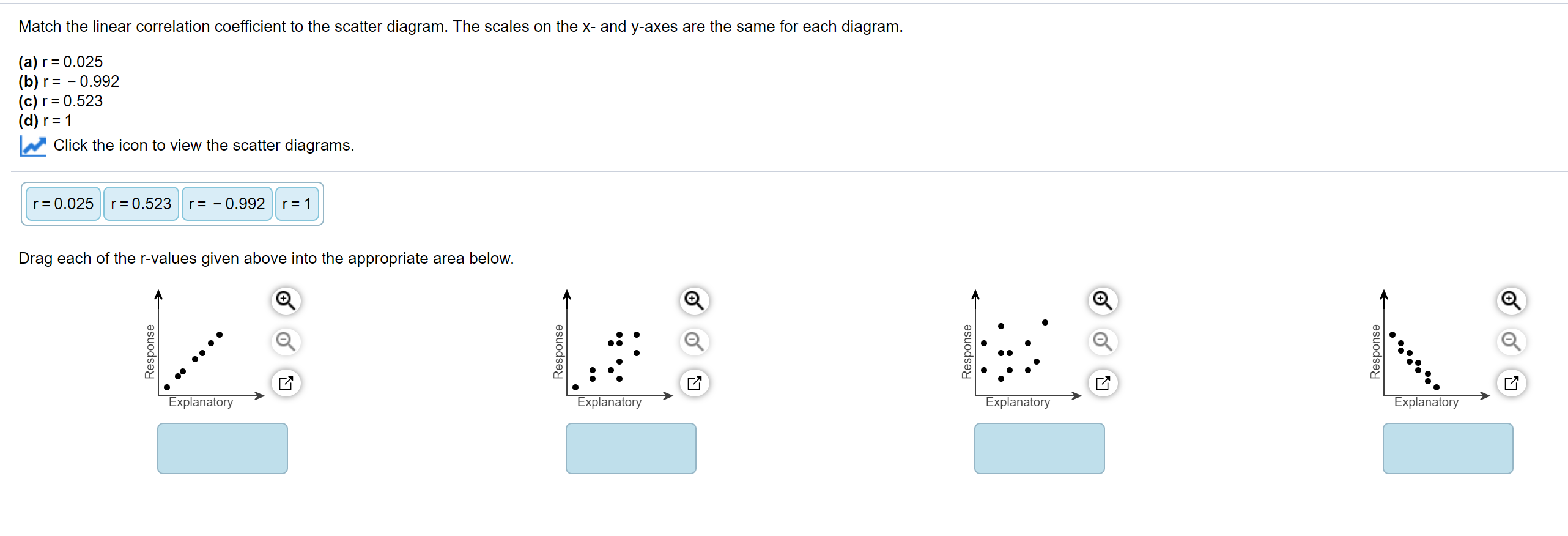




0 Response to "36 match the linear correlation coefficient to the scatter diagram."
Post a Comment